《2》整音作業によって変化する音色要素の説明
|
|
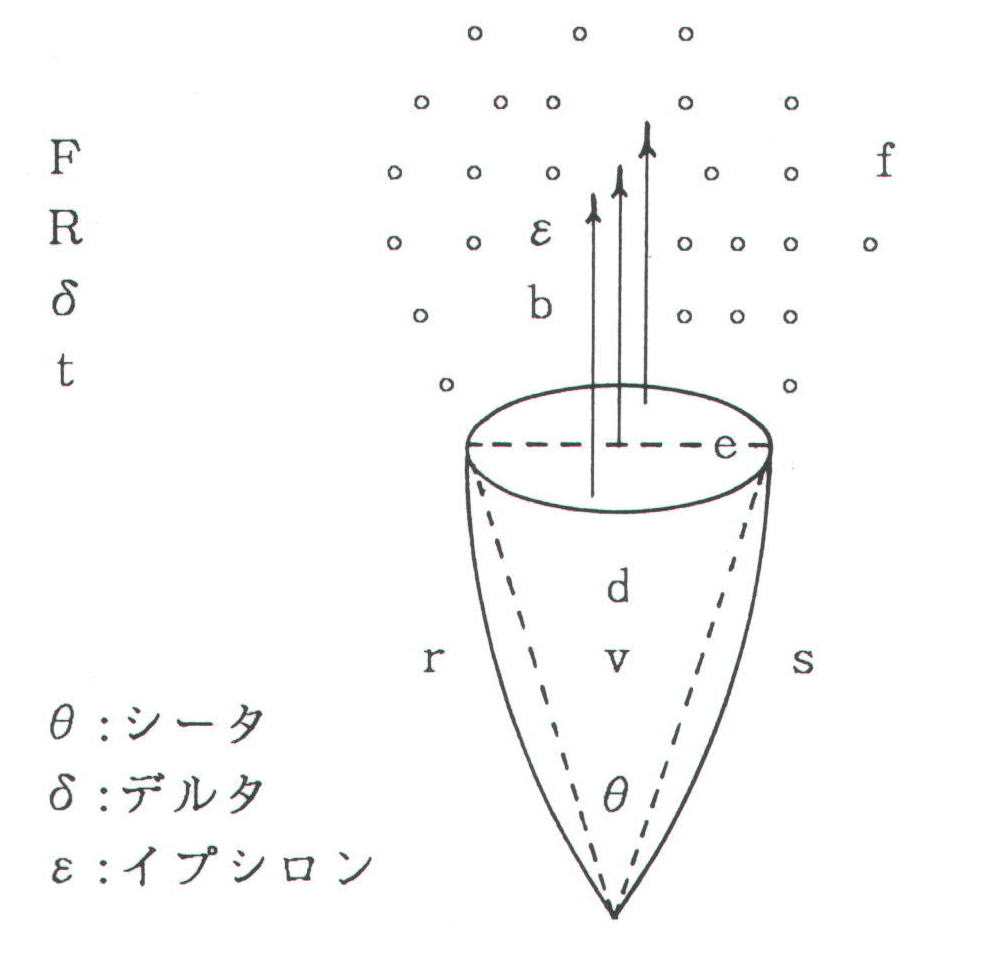
上のの立体図形をじっくりご覧頂きたい。この図形は音色要素を立体図形として表示したものであり、一対
一対応をしている。θ,r,s,d,f,ε(ε∈b) の整音作業によって静体図形が変化する代表的な6個の
音色要素を示した。 これに時間軸の概念を導入すると更にt,v,δ,e の主なる4個の動体要素が加わ
る。整音作業によって動体音色要素vは変化するがt,δ,eは変化しない。 ここに掲げた構成要素は総て感
覚で捕える事が可能な固有の性格を持った要素である。
整音とはこの(θ,r,s,d,ε,f,v)7個の音色要素の「理想的な値」と「理想的な相関関係」
を作り出す作業とも言える。(b の説明はεの項目を参照 )
静体要素の係数(θ,r,s,d,ε,f,Γ)について
θ 開口部の口の開き具合を表す係数。
音の母音の変化を表す要素である。開口部が完全に開いているものは音の輪郭を捕える事が出来ず球面波
のように聴こえてくる。θが小さくなればなるほど音に気品が増してくる。段階的に母音で説明するとア
ー、エー、イー、ウー、オー、である。ここでアー、エー、イー、で響くのは極めて下品な音色で聴くに
堪えない。ウーで心地よく響く場合も多々あるのでオーでなくてはならない理由はない。音像が完全に閉
じている場合には音が真上に抜けて行く感じがする。またffで和音を弾くと束になって真上に抜けていく。
この状態は静体図形の輪郭線がくっきりと見えている。
r立体図形の側面の曲率を表す係数
値が大きくなるほど図形側面の膨らみが増し、音に 「まろやかさ」が増して来る。rの値が大きくなりす
ぎると音像はぼやけてffで力がなくなる。
s 立体図形の表面の質感を表す係数。
滑らかで深みがあり肉厚が薄く輪郭線がくっきりしているほど音の「質感」を良しとする。理想的なsの
値では、音にきめ細かな「艶」を感じる。ハンマー先端部分の密度が低いと側面の輪郭線がぼけて器に硬
度がなく肉厚が厚い。音にベールが掛かっている状態。逆に密度が高すぎると器の輪郭線はザラ付いて肉
厚も厚く堅く感じる。音は刺激的で耳が疲れるこれは私の感覚であるが、表面の質感については磁器なり
陶器で出来た無地の壷を想像するのが最も適している。これは無数と言ってよいほどの種類、質感の器が
存在するからである。ここで私が最上とするものは中国南宋初期の青磁である。汝窯、龍泉窯、郊壇官窯
などのいわゆる砧青磁と言われるものである。表面の質感、品位、その曲線といい極めて洗練されている。
古今東西これ以上の器は存在しない。私は整音作業をするにあたり、理想のr,sの値をこれらの青磁に
求めている。
d 立体図形の中身の密度を表す係数。
値が小さい場合は物足りなさを感じ、適度な場合は音にしっかりとした芯がある。値が大きくなりすぎる
とffで音像が潰れ、香りも消える。しかしこのdは次に説明するεとは本質的に違う要素でdの値が増え
てもいわゆる「鳴りの良いピアノ」には変身しない。あくまでも音に芯があるかないかを表す要素である。
ε の値の違いで響板の震動の仕方が著しく変化する。聴感上の差が顕著でいわゆる「鳴りの良いピアノ」
に変身する。これは立体図形の変化としてではなく、放射される音波の単位面積当たりの密度の変化とし
て捕らえる。εの値が増すにつれ、音に「コクと旨味」が出てくる。この「コクと旨味」成分はメーカー
を問わず総てのピアノに内在しているがこの成分が顕著に音として出ているピアノに出あった事は殆んど
無い。CD盤、LP盤でさえ今迄にわずか十数枚である。ピアノに問題があるわけではなく、整音技術に
問題がある。この「コクと旨味」成分を出す事は至難の技で、極めて高度な整音技術を要する。「コクと旨
味」成分をbと定義すれば ε∈b の関係が成り立つ。この数式は《「コクと旨味」成分は「鳴りのよい
ピアノ」に変身させない限り絶対に出す事は出来ず、また「鳴りのよいピアノ」に変身させたからと言っ
て決して出てくるとは限らない》と言う事を意味する。ε と言う部屋のなかに bと言う手放し難い宝物
が密かに隠されている、と言う事を意味する。
f 図形周囲に充満する点の粗密を表す係数。
単位体積あたりの点が多いほど香りが濃い。可聴周波数以上の楽音としての倍音が出る程fの値は大きく
なり、香りが濃くなる。fは整調によって大きく変化するがRも同時に変化してしまう。f-R の関係が
密接に作用しあっているので整音前の整調には相当の神経を使わなくてはならない
Γ(a,b,c,d,〜)
θ,r,s,d,ε,f以外の整音作業によって実際には変化しているが感知できない静体要素群の集合
を表す。
動体要素の係数(t,v,Δ)について
t 打弦後の音の発音から消滅までの時間の長さを表す係数。
v 立体図形の体積を表す係数。
音の大きさの推移を体積vの変化の推移として捕える。v−t曲線は音楽を表現するうえで極めて重要な
曲線である。完璧に整音されたピアノの音は打鍵、約0.8 秒後にふわっとした山がでてくる。この山があ
るか無いかで説得力がまるで違ってくる。レントでしかもメロディーラインがはっきりしている曲につい
てはその差が顕著である。山のあるものは一つ一つの音が心に問いかけ、迫ってくるものがある。 また
v−d−ε の相関関係が理想的な場合、音に心地よい「ねばり」を感じる。
Δ(a,b,c,d,〜)
v以外の整音作業によって変化する動体要素群の集合を表す。
![]()